介绍几种常用的排序算法:选择,冒泡,插入,归并,快排,堆排,希尔,计数
各种排序的时间复杂度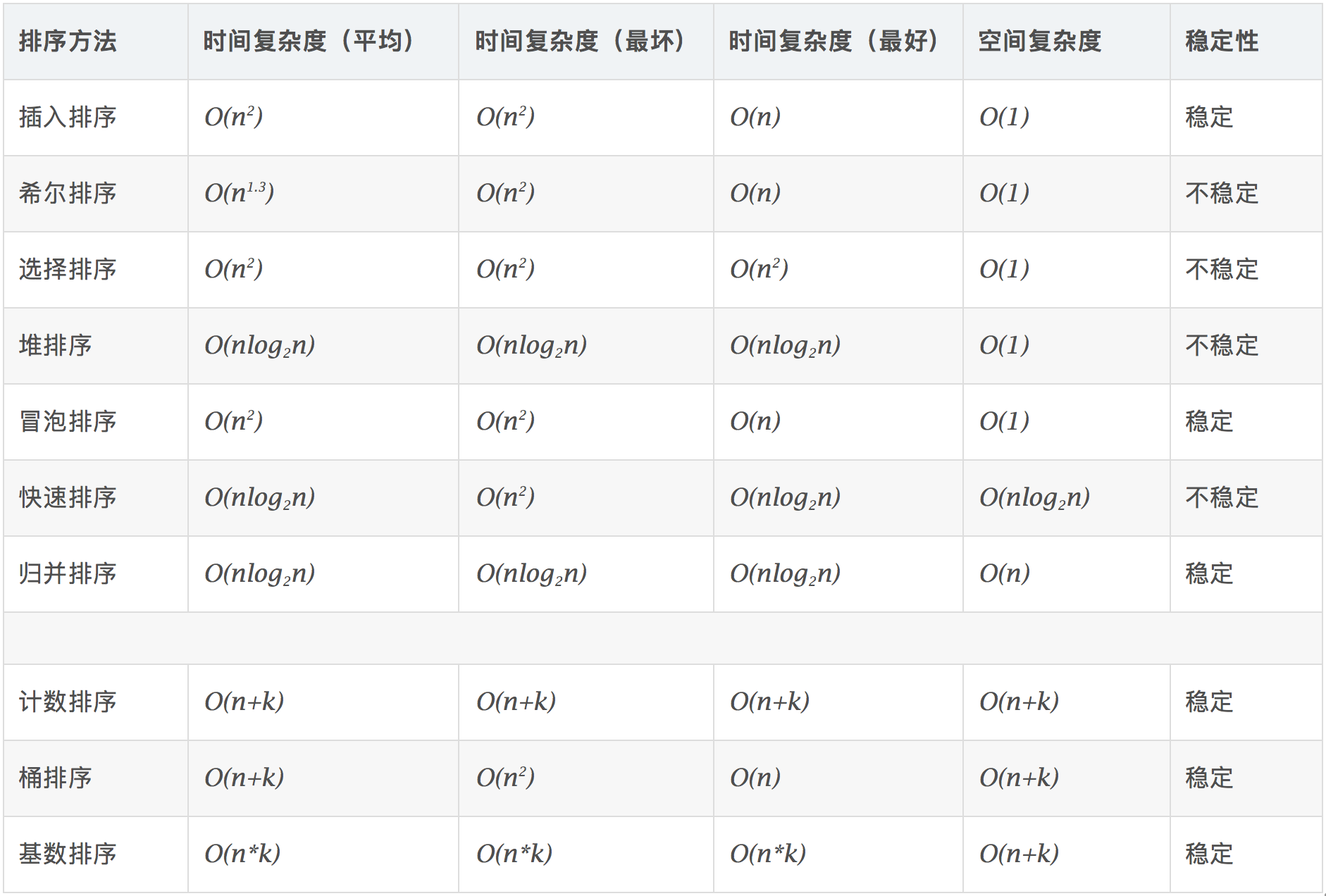
冒泡
冒泡:时间复杂度最优O(n),平均&最坏O(N^2);稳定的排序算法
通过每次遍历一次序列,两两交换,正确性显而易见:每一次遍历都会有一个数放在它该在的位置,一个数至多交换n次,适用于短序列排序
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20public static int[] bubble(int[] nums){
if(nums.length<2){
return nums;
}
for (int i = 0; i <nums.length-1 ; i++) {
//优化操作,如果不在交换,证明已经排好了序
boolean isSwap=false;
for (int j = 0; j <nums.length-i-1 ; j++) {
if(nums[j]>nums[j+1]){
swap(nums,j,j+1);
isSwap=true;
}
}
if(!isSwap){
return nums;
}
}
return nums;
}
选择排序
不稳定,时间复杂度:最优O(N),平均&最坏O(N^2)
每次选择剩余序列中最小的一位,保证i之前部分有序,适用于短序列排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16public static int[] selectSort(int[] nums){
if (nums.length<2){
return nums;
}
for (int i = 0; i <nums.length-1 ; i++) {
int minIndex=i;
for (int j =i+1; j <nums.length ; j++) {
if(nums[j]<nums[minIndex]){
minIndex=j;
}
}
swap(nums,i,minIndex);
}
return nums;
}
插入排序
最佳情况:T(n) = O(n),最坏&平均:T(n) = O(n^2)
保证前i个数有序,适用于短序列排序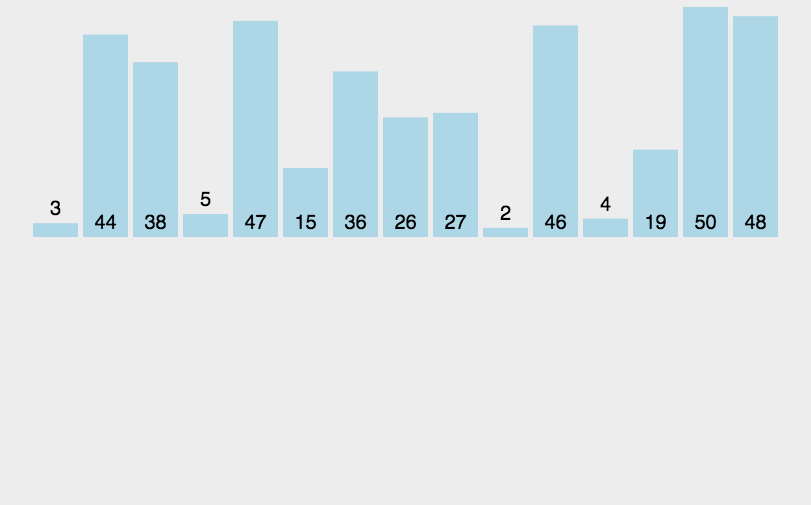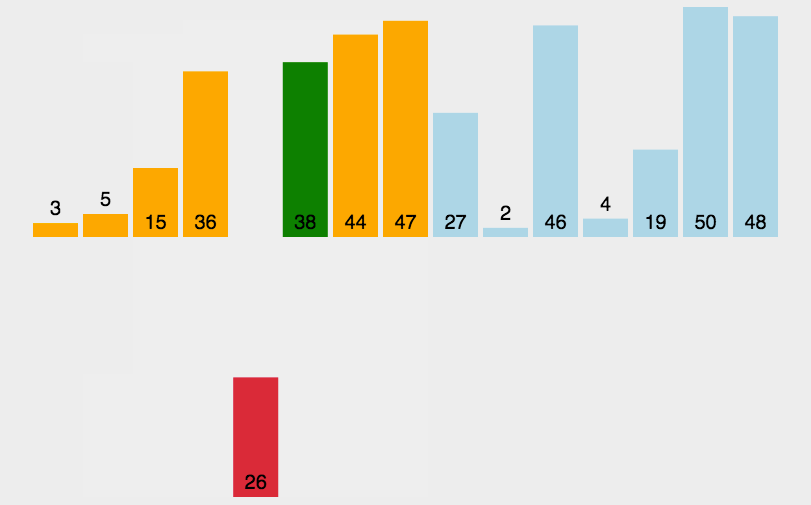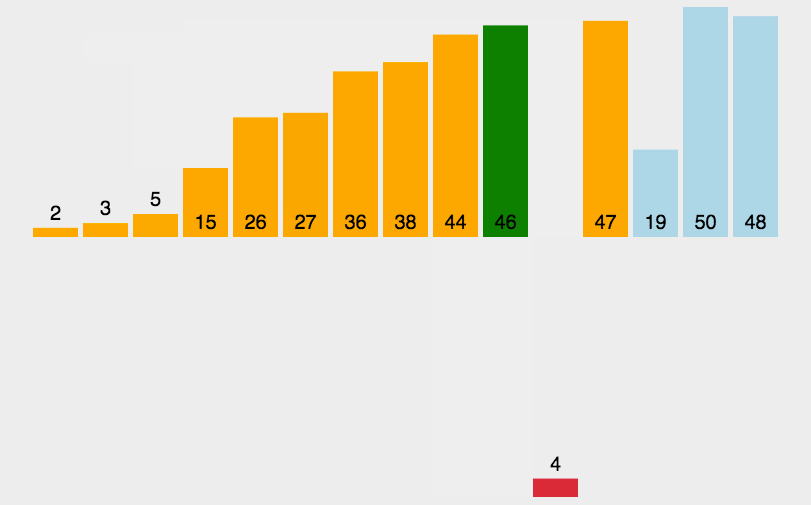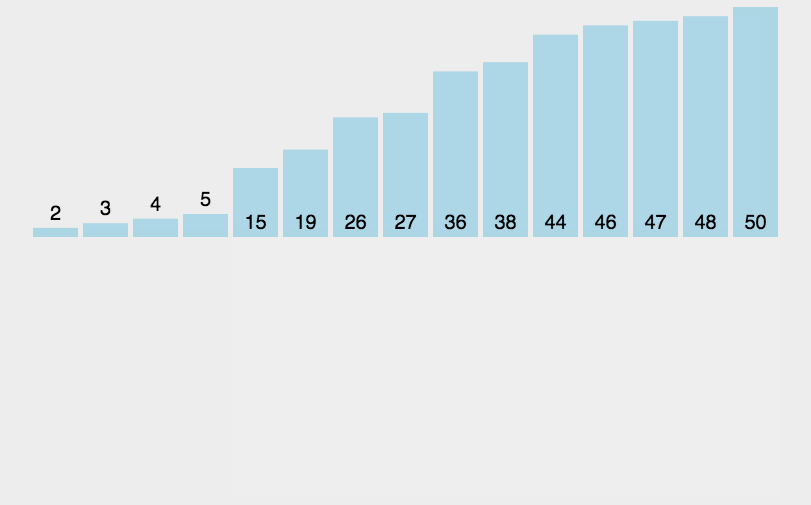
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17public static int[] insertSort(int[] nums){
if (nums.length<2){
return nums;
}
for (int i = 1; i <nums.length ; i++) {
int curr=nums[i],j=i-1;
//找到位置,插入
while (j>=0&&nums[j]>curr){
nums[j+1]=nums[j];
--j;
}
nums[j+1]=curr;
}
return nums;
}
希尔排序
最佳&最坏&平均:T(n) = O(nlog2 n)
保证每一个分组有序,最后合并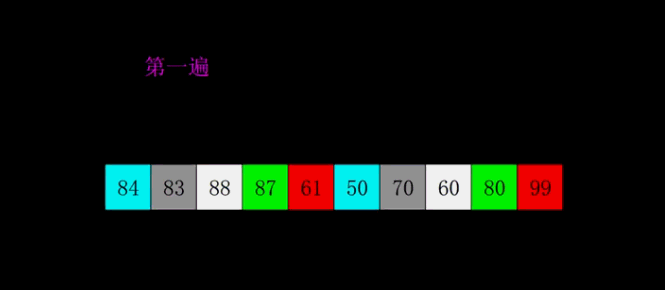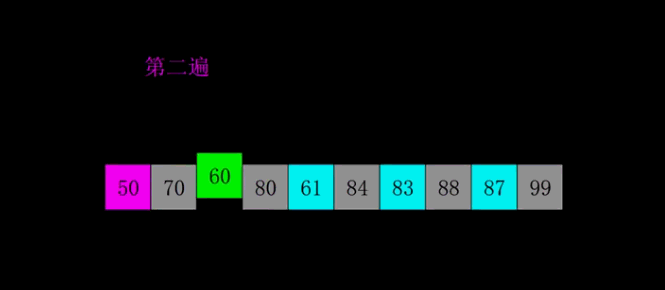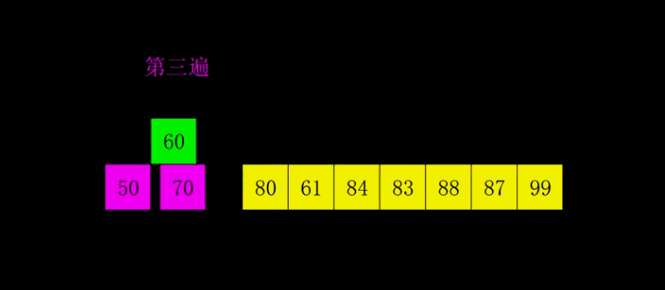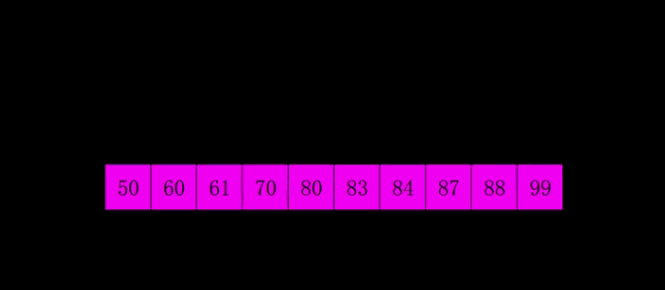
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public static int[] shellSort(int[] nums){
if(nums.length<2){
return nums;
}
int group=nums.length/2;
//分组排序
while (group>0){
for (int i = group; i <nums.length ; i++) {
int curr = nums[i], preIndex = i - group;
while (preIndex >= 0 && nums[preIndex] > curr) {
nums[preIndex + group] = nums[preIndex];
preIndex -= group;
}
nums[preIndex + group] = curr;
}
group/=2;
}
return nums;
}
归并排序
最优&最坏&平均时间复杂度O(NlogN)
分治思想
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31public static int[] mergeSort(int[] nums){
if(nums.length<2){
return nums;
}
int mid=nums.length/2;
int[] left=Arrays.copyOfRange(nums,0,mid);
int[] right=Arrays.copyOfRange(nums,mid,nums.length);
return merge(mergeSort(left),mergeSort(right));
}
private static int[] merge(int[] left, int[] right) {
int[] res=new int[left.length+right.length];
int i=0,j=0,k=0;
while (i<left.length&&j<right.length){
if(left[i]<=right[j]) {
res[k++] = left[i++];
}else {
res[k++]=right[j++];
}
}
while (i<left.length){
res[k++]=left[i++];
}
while (j<right.length){
res[k++]=right[j++];
}
return res;
}
堆排序
最佳&最好&平均T(n) = O(nlogn)
堆排序在求TopK时更适用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39public static void heapSort(int[] nums){
if(nums.length<2){
return;
}
//建堆
buildMaxHeap(nums);
//首尾交换,直至长度为0
int len=nums.length;
while (len>0){
swap(nums,0,len-1);
len--;
adjustMaxHeap(nums,0,len);
}
}
//调整堆
private static void adjustMaxHeap(int[] nums, int i,int limit) {
int maxIndex=i;
if(i*2<limit&&nums[i*2]>nums[maxIndex]){
maxIndex=i*2;
}
if(i*2+1<limit&&nums[i*2+1]>nums[maxIndex]){
maxIndex=i*2+1;
}
if(maxIndex!=i){
swap(nums,i,maxIndex);
//向下适应
adjustMaxHeap(nums,maxIndex,limit);
}
}
private static void buildMaxHeap(int[] nums) {
for (int i = (nums.length-1)/2; i >=0 ; i--) {
adjustMaxHeap(nums,i,nums.length);
}
}
快排
最佳&平均:T(n) = O(nlogn),最差:T(n) = O(n^2)
快排主要使用了分治的思想,每一次都将原问题缩小为1/2
1 | public static void quickSort(int[] nums,int start,int end){ |
计数排序
复杂度:O(max-min),适用于比较密集的数据,而且最大值和最小值不能相差太大,不然浪费空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21//计数
private static void countSort(int[] nums){
int min=Integer.MAX_VALUE;
int max=Integer.MIN_VALUE;
for (int a:nums){
max=Math.max(a,max);
min=Math.min(a,min);
}
int[] help=new int[max-min+1];
for (int a:nums){
help[a-min]++;
}
int k=0;
for (int i = 0; i <help.length ; i++) {
if (help[i]!=0){
while (help[i]-->0){
nums[k++]=i+min;
}
}
}
}
bogoSort
神奇的算法,运气排序
1 | private static void bogoSort(int[] nums){ |
除了这些算法,还有很多有趣的算法,比如timSort:java,python等内置排序算法,稳定高效;
双基准快排:java内置排序算法
桶排序,鸡尾酒排序,煎饼排序…
图片来源于:https://www.cnblogs.com/onepixel/articles/7674659.html
